
El interés compuesto es el interés que suma sobre el capital inicial más el rendimiento que produce. Esto quiere decir que el dinero se acumula y sobre esa nueva base se producen los nuevos rendimientos, de esta manera los ahorros crecen exponencialmente. El rendimiento es más alto, por lo que lo convierte en el complemento perfecto para la pensión de jubilación.
La Seguridad Social estableció en 8,9 millones el número de pensionistas que había en España en el año 2021. El grueso de estos son jubilados y la mayoría cobran un 72,3 % de su última nómina, según la Organización para la Cooperación y el Desarrollo Económico (OCDE). Estos números llevan a los retirados a perder parte de su poder adquisitivo, por lo que muchos optan por complementar su pensión y eligen el interés compuesto.
A largo plazo, este complemento financiero permite ahorrar dinero. En definitiva, es una fórmula matemática que permite al inversor obtener más rendimientos a largo plazo, ya que su beneficio se reinvierte. Este tipo de interés también se conoce como efecto bola de nieve porque el dinero crece a medida que pasa el tiempo, como la bola de nieve que aumenta su volumen cuando rueda colina abajo.
Por último, es importante recordar que para disfrutar de los beneficios de este interés hay que esperar un tiempo. Si la metáfora de la bola de nieve se tiene en mente, hay que dejar rodar durante un período para que los rendimientos financieros crezcan.
El interés compuesto y ejemplos
Por definición, es interés compuesto acumula rendimientos sobre los resultados de los rendimientos anteriores. Por lo que acumula riqueza a largo plazo, ya que el interés se suma al capital inicial y sobre este resultado se generan nuevos beneficios. Las características detalladas de este complemento:
- Crecimiento del capital inicial en cada período porque se acumulan los intereses
- El capital sobre el que se aplica la tasa de interés va creciendo
- Aumentan los intereses en cada período a causa de las reinversiones
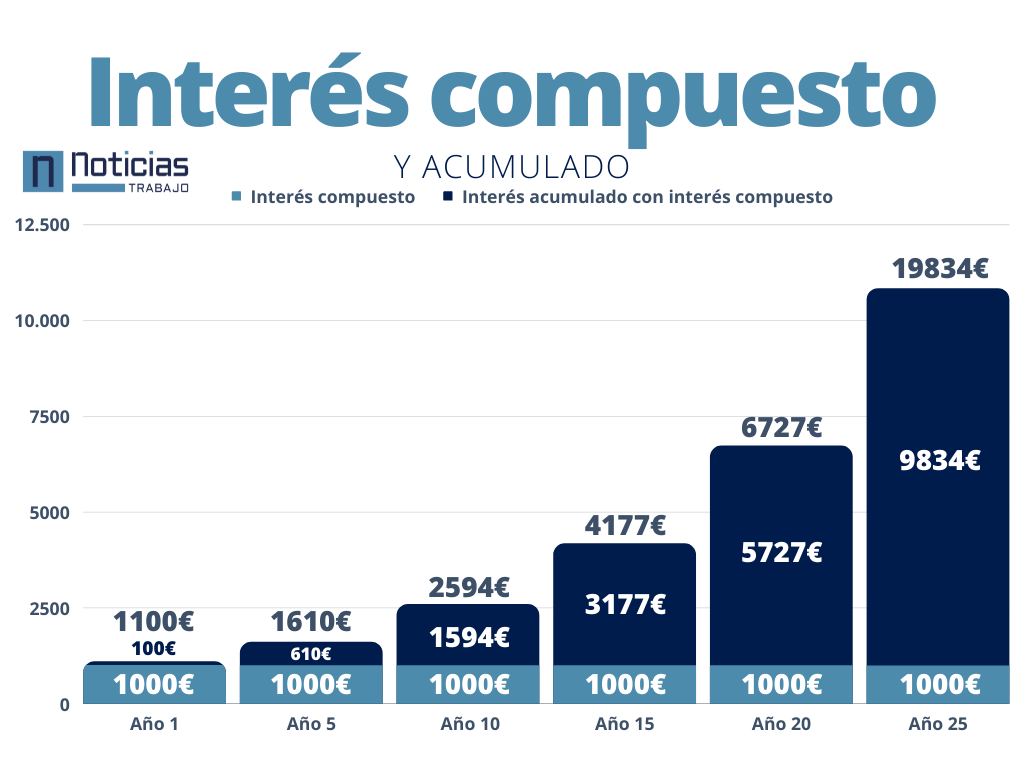
Un ejemplo para ayudar a ver los resultados antes de explicar la fórmula matemática que se aplica para calcular el interés compuesto. El caso supuesto se estudia a partir de una base de 1.000 euros con un interés compuesto del 10 %. Después de un año, los intereses que se generan asciende a 100 euros.
Si el dinero que se obtiene de la suma, 1.100 euros, no se saca de la cuenta bancaria y se mantienen las mismas condiciones, al año siguiente los beneficios ascienden a 1.210 euros. Ya que la base sobre la que se calcula el nuevo interés es 1.100 euros, el segundo año se obtienen mayores beneficios porque el interés se acumula.
Pasados 10 años, si las condiciones se mantienen, un interés del 10 % al año y no se saca el dinero, el interés habrá crecido hasta 2.594 euros. La cantidad de beneficio generado asciende a 3.594 euros, como vemos, el interés compuesto a lo largo de un período largo de tiempo genera una cantidad de dinero que supera en el doble a la cantidad inicial que se invirtió.
Cálculo del interés compuesto
La fórmula matemática por la que se calcula el capital final resulta de multiplicar el capital inicial por la tasa de interés más uno, todo ello elevado al período de tiempo que dura la inversión. En lenguaje matemático es la siguiente:
Capital final = C0 x (1+Ti) ^t
*Capital inicial (C0), tasa de interés anual (Ti), período de tiempo que dura la inversión (^t)
El ejemplo que se va a utilizar es el explicado en el apartado anterior, es decir, mi capital inicial es de 1.000 euros, el interés compuesto un 10 % y el período de tiempo 1 año. Si por definición el interés compuesto acumula rentabilidades sobre las rentabilidades anteriores, se va a calcular aplicando la fórmula el capital final después del primer año.
Capital final = 1000 x (1+0,1/1) ^1= 1.100 euros
Ahora se estudia el supuesto a lo largo de 10 años, el capital inicial 1.000 euros y el interés de un 10 %
Capital final= 1000x(1+0,1/0,1)^10= 2.593,7 euros
El interés compuesto es aliado si son operaciones de inversiones, en caso de préstamos se convierte en un enemigo porque afecta al prestado directamente. También recordar que es un rendimiento a largo plazo, por lo que no interesa si se quieren obtener rendimientos de forma rápida. Además, el interés compuesto es un producto que ofrece la mayoría de los bancos, por lo que los pensionistas no tendrán problemas para acceder a este beneficio.
Lo más leído
-
Precio de la luz mañana sábado, 20 de abril de 2024: cuándo es más barata y más prohibitiva
-
Buenas noticias para los herederos: no tendrán que pagar a Hacienda este impuesto en 2024
-
Ofertas de empleo hoy 19 de abril con contrato indefinido: hasta 50.000 euros de sueldo
-
Hacienda tiene que devolver hasta 4.000€ del IRPF a miles de jubilados: cómo solicitarlo
-
Adiós a la pensión de jubilación aún con 15 años cotizados: cómo evitarlo
